Graph Basic Theory
1.그래프의 정의
그래프란 vertex와 edge로 구성되어 있다.
vertex(정점)은 node(노드)와 비슷한 의미이며 보통의 그래프 그림에서 동그란 부분을 의미한다.
edge(간선)은 정점들의 연결 관계를 의미하며 보통의 그래프 그림에서 실선을 의미한다.
이러한 vertex 들의 집합을 V , edge 들의 집합을 E 라고 할때 그래프 G(V,E) 라고 표현한다.
2.그래프의 종류
2-1.일반적인 분류
그래프는 크게 두 가지로 분류될 수 있다.
방향(유향) 그래프(directed graph) 와 무방향(무향) 그래프(undirected graph)가 있다.
방향 그래프와 무방향 그래프는 말 그대로 한 정점에서 다른 정점으로 이동할때 방향에 제약이 있는지 없는지의 차이다.
방향 그래프의 예
무방향 그래프의 예
만약 방향 그래프이던 무방향 그래프이던 간선(Edge)에 가중치가 붙으면 가중치 그래프(weighted graph)가 될 수 있다.
가중치 그래프의 예
2-2.특수한 경우
만일 정점들 사이에 간선이 2개 이상이면 해당 그래프를 다중 그래프(multigraph)라고 부르며,
정점의 간선관계를 그룹으로 분할하는데, 2그룹으로 분할된다면 이분 그래프(bipartite graph)라고 부른다.
마지막으로 그래프는 간선의 형태에 따라 트리와 다르게 순환(cycle)이 생길 수 있다. 그러나 그래프에서 순환이 없는경우 이를
DAG(directed acycle graph) 라고 부른다.
다중 그래프의 예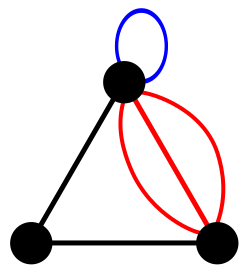
이분 그래프의 예
DAG의 예
3. 그래프의 표현 방법
그래프의 표현 방법에는 2가지가 있다. 첫 째로 인접 행렬이 있다. 인접 행렬 방식은 미리 N,M크기의 2차원 배열을 잡고 시작한다. 두번째로 인접 리스트가 있다.
눈치가 있다면, 인접 행렬은 공간을 많이 낭비하고, 인접리스트는 필요한 만큼만 공간을 할당한다.
"인접 행렬은 배열을 사용하고 인접 리스트는 링크드 리스트를 사용하는것이 아니다!!"
본래 사람이 이해하기 쉬운 그래프
인접 행렬 표현
int G[500][500];
인접 리스트의 표현
vector<list<int>>
vector<vector<int>>
그렇다면 먼저 인접행렬과 인접리스트중에 어떤것을 선택해야할까?
간단하게 설명하자면 인접행렬은 index로 접근이 가능하기 때문에 Graph알고리즘을 수행할때 복잡도가 더 빠르게 나오는 경우가 있다. 다만 공간을 많이 차지한다.
인접 리스트는 공간을 필요한 만큼만 차지하지만, 첨자접근이 안되기때문에 복잡도계산에서 불리할 수 있다.
만일 간선의 수가 정접의 제곱에 가까워지면 인접행렬을 쓰는것이 유리하다.
(어차피 공간을 VxE만큼 사용하기 때문)
실제 PS에서 그래프 문제이지만 그래프를 만들 필요는 없다.
이미 DFS나 BFS를 써본 경험이 있다면, 굳이 위의 그래프를 만들지 않고도 수행할 수 있음을 알고있을 것이다. 적절한 상황에 맞게 사용하는것이 핵심이다.
Copyright (C) 2016 (KimBom) all rights reserved.